
Some machines store the two bytes of a 16-bit word least significant byte first (so-called little-endian machines) and some store most significant byte first (big-endian machines).Unicode is a character set.
Use the pattern 110110xxxxxxxxxx 110111xxxxxxxxxx bin to encode the upper- and lower- 10 bits into two 16-bit words. U+10000 to U+10FFFF uses 4-byte UTF-16 encoded as follows: U+E000 to U+FFFF uses 2-byte E000 hex to FFFF hex U+D800 to U+DFFF are invalid codepoints reserved for 4-byte UTF-16 U+0000 to U+D7FF uses 2-byte 0000 hex to D7FF hex UTF-16 uses 2 or 4 bytes to represent Unicode codepoints. Or if nul-terminated strings are desired: Your codepoints are U+006D, U+0416 and U+4E3D requiring 1-, 2- and 3-byte UTF-8 sequences, respectively. †Unicode codepoints are undefined beyond 10FFFF hex. Follow on bytes always start with the two-bit pattern 10, leaving 6 bits for data:Ģ-byte UTF-8 = 110xxxxx 10xxxxxx bin = 5+6(11) bits = 80-7FF hexģ-byte UTF-8 = 1110xxxx 10xxxxxx 10xxxxxx bin = 4+6+6(16) bits = 800-FFFF hexĤ-byte UTF-8 = 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx bin = 3+6+6+6(21) bits = 10000-10FFFF hex † The initial byte of 2-, 3- and 4-byte UTF-8 start with 2, 3 or 4 one bits, followed by a zero bit. For the 1-byte case, use the following pattern:ġ-byte UTF-8 = 0xxxxxxx bin = 7 bits = 0-7F hex UTF-8 uses up to 4 bytes to represent Unicode codepoints. Procedures for your example string: UTF-8 The descriptions on Wikipedia for UTF-8 and UTF-16 are good: There is an x spot left over at the start, fill it in with 0: 11100100 10111000 10111110 Drop the bits into the x above (start from the right, we'll fill in missing bits at the start with 0): 1110x100 10111000 10111110 Once you have built the chart above, you can convert input Unicode codepoints to UTF-8 by finding their range, converting from hexadecimal to binary, inserting the bits according to the rules above, then converting back to hex: U+4E3E Here's hoping you're good at remembering rules too. 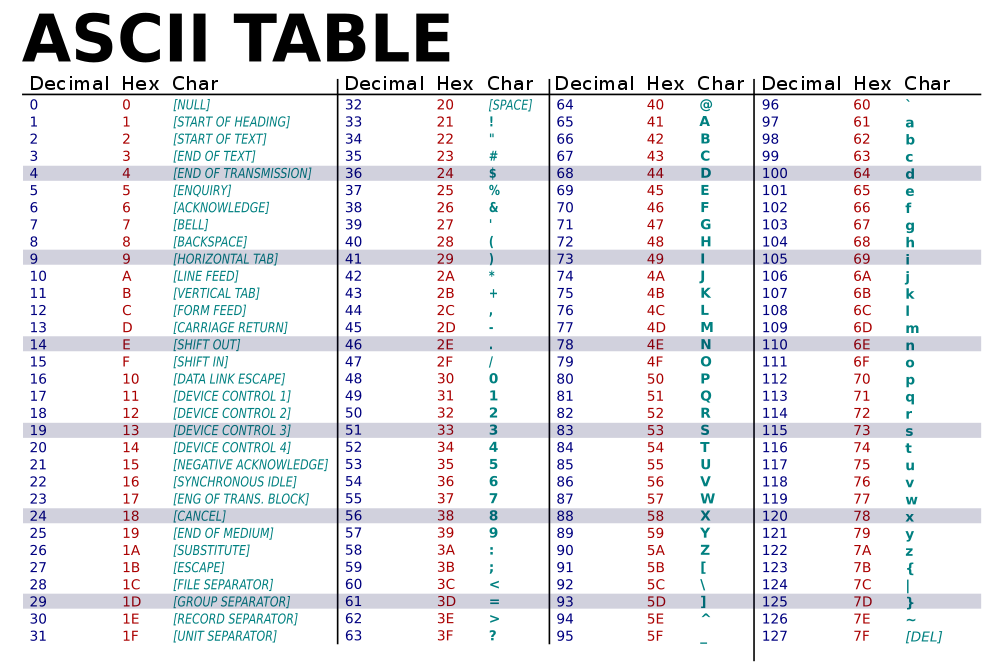
I know I could remember the rules to derive the chart easier than the chart itself. You can derive the ranges by taking note of how much space you can fill with the bits allowed in the new representation: 2**(5+1*6) = 2048 = 0x800 Initial bytes starts of mangled codepoints start with a 1, and add padding 1+0. It might be easier to remember a 'compressed' version of the chart:
UTF 16 CODEPOINTS TO UTF 8 TABLE CODE
The UCS code values 0xd800–0xdfff (UTF-16 surrogates) as wellĪs 0xfffe and 0xffff (UCS noncharacters) should not appear in Shortest possible multibyte sequence which can represent theĬode number of the character can be used. The xxx bit positions are filled with the bits of theĬharacter code number in binary representation.
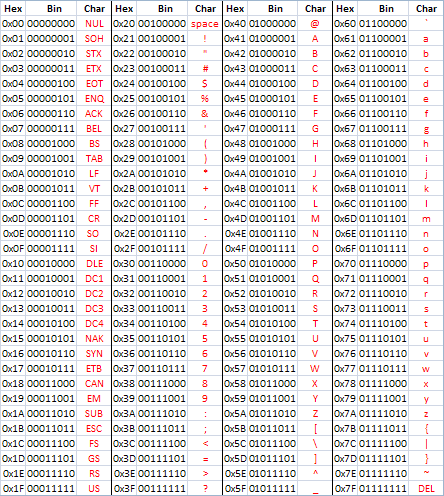
The sequence to be used depends on the UCS code The following byte sequences are used to represent aĬharacter. The clearest description I've seen so far for the rules to encode UCS codepoints to UTF-8 are from the utf-8(7) manpage on many Linux systems: Encoding (Will it help students pass the Turkey test?) On the one hand I'm thrilled to know that university courses are teaching to the reality that character encodings are hard work, but actually knowing the UTF-8 encoding rules sounds like expecting a lot.







 0 kommentar(er)
0 kommentar(er)
